Joining the group
In der Gruppe gibt es fortlaufend Themen für Bachelor- und Masterarbeiten, u.a auch in möglicher Kooperation mit der AG Otto (angewandte Physik, zelluläre Biophysik) (Information). Wenn Sie sich dafür interessieren, Teil der Arbeitsgruppe zu werden, oder auch nur einen Einblick in die aktuelle Forschungsarbeit wünschen, kontaktieren Sie gerne Prof. Thomas Ihle oder Dr. Horst-Holger Boltz.
There are always topics for bachelor or master theses in the ongoing research within the group. If you are interested or just want to get in touch, please contact Prof. Thomas Ihle or Dr. Horst-Holger Boltz
Statistical physics of active matter
Biological "units" (cells, bacteria, animals, units, …) are out of equilibrium: there is an energy uptake from the environment that is translated into activity, examples of which are motion or the generation of stresses. Active matter is a conceptual term for systems that are comprised of such active units. As the energy source as well as the specific machinery that generates the activity are often not explicitly modelled, such active matter systems are to an extent outside the paradigms of standard statistical physics, for example usual conservation laws for energy or momentum may not hold.
The general type of questions is very similar: Given a specific set of dynamical rules (equations of motion), what behaviour would one observe in a large ensemble of these systems? Consequently, techniques from standard passive statistical physics can be adapted towards active matter. Any analytical description has to deal with the abundance of information in these systems, actually tracking the evolution of every microscopic degree of freedom is generally neither feasible nor constructive. Identifying the relevant information (often in form of slow modes) is, therefore, an essential task. This step is often guided by numerical insight into the model via simulation. Having identified a physically interesting set of variables, reduction of the model then constitutes a technical challenge: We explicitly want to neglect information about the system and describe it solely in terms of the interesting variables. Working along these lines, might for example result in the effective description of a deterministic system being stochastic, with a noise term originating in the reduced description.
Addressing both aspects, is by no-means straightforward and the way to a efficient and insightful treatment problem-specific, which results in broad variety of approaches.
Kinetic theory of swarms and flocks

Swarms and flocks are concepts of biology that have generalized counterparts in active matter physics. In a system of actively moving, self-propulsing particles (which could be considered as modelling birds or swarm insects) that are interacting, collective phenomena can occur on a macroscopical level. For example, particles can aggregate and move collectively as macroscopically large flocks into a specific direction.
We approach the interesting emerging collective, macroscopic properties from the direction of kinetic theory. Meaning we derive the evolution of macroscopic (or mesoscopic) properties directly from explicit microscopic dynamical rules.
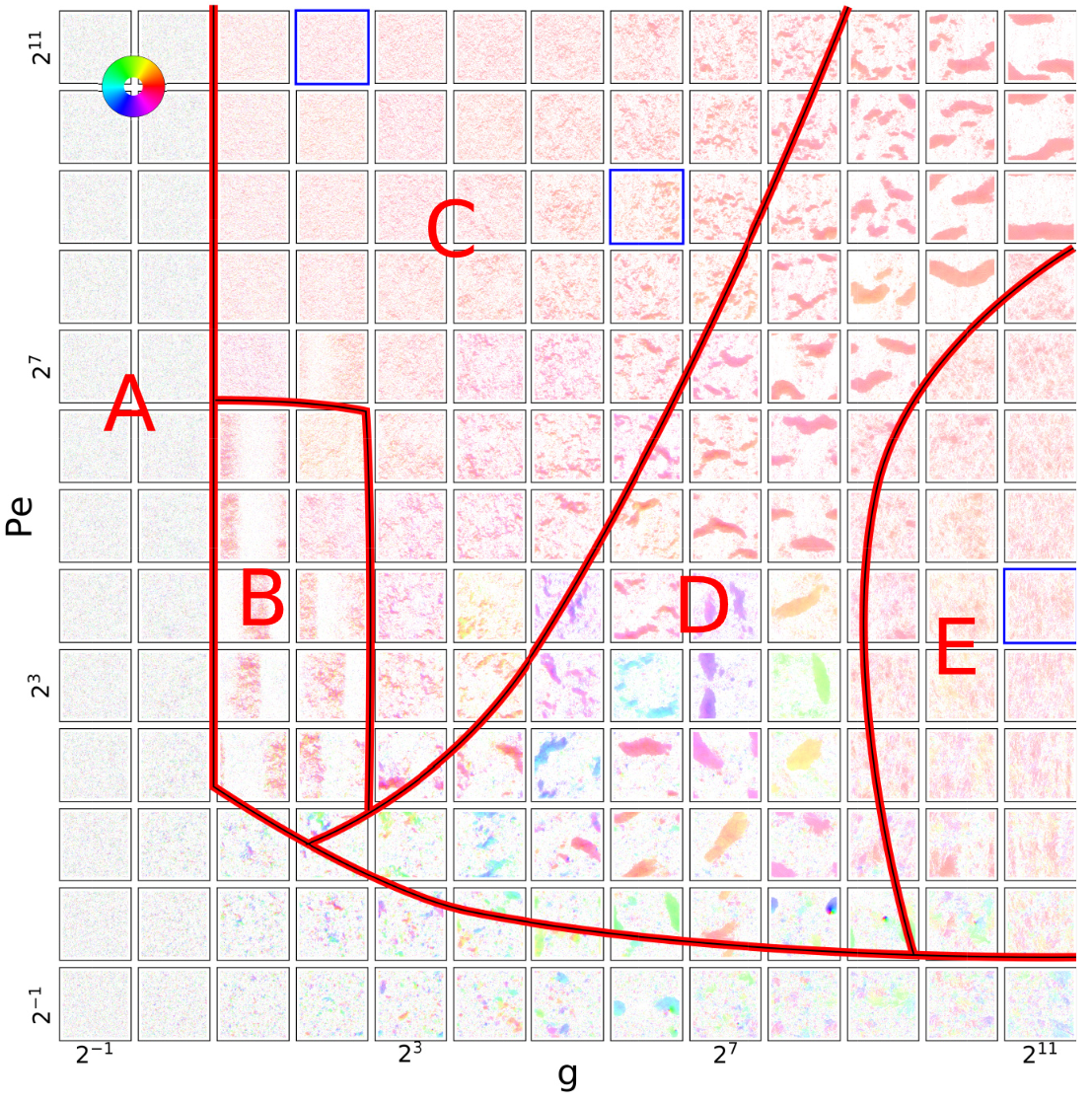
As active matter offers an abundance of paradigmatically novel phenomena and challenges, there is value in understanding minimalistic models. One is Vicsek model of flocking, self-propulsing particles that try to align with the average direction of motion of their immediate neighbors. For this model, we derived the hydrodynamic equations from a Enskog-type kinetic theory. From a theoretical perspective, it is crucial that mean-field-type descriptions often fail to adequately describe active matter systems and correlations explicitly have to be considered, for example by means of ring-kinetic theory.
Recently, we have shown by means of numerical study of very large systems that there exists a cross-sea phase in the Vicsek model, an independent complex pattern of crossing bands with polar order.
Vicsek-model like systems can have peculiar relaxational properties (Giant Kovacs-like memory effect) that are more usually found in disordered systems, as we have shown from a non-linear theory.
Aside from flocking, agents might also actively try to avoid each other. Such social distancing can for example be modeled by anti-aligning interactions. In two recent publications (short with main results, longer with full explainations), we have shown how to explicitly build a quantitative scattering theory for such a system, for which the mean-field or molecular chaos description fails. This is based on a non-local closure, the one-sided molecular chaos approximation, that explicitly accounts for the (compressible) flow of probability and correlation during pair interactions.
Soft condensed matter physics
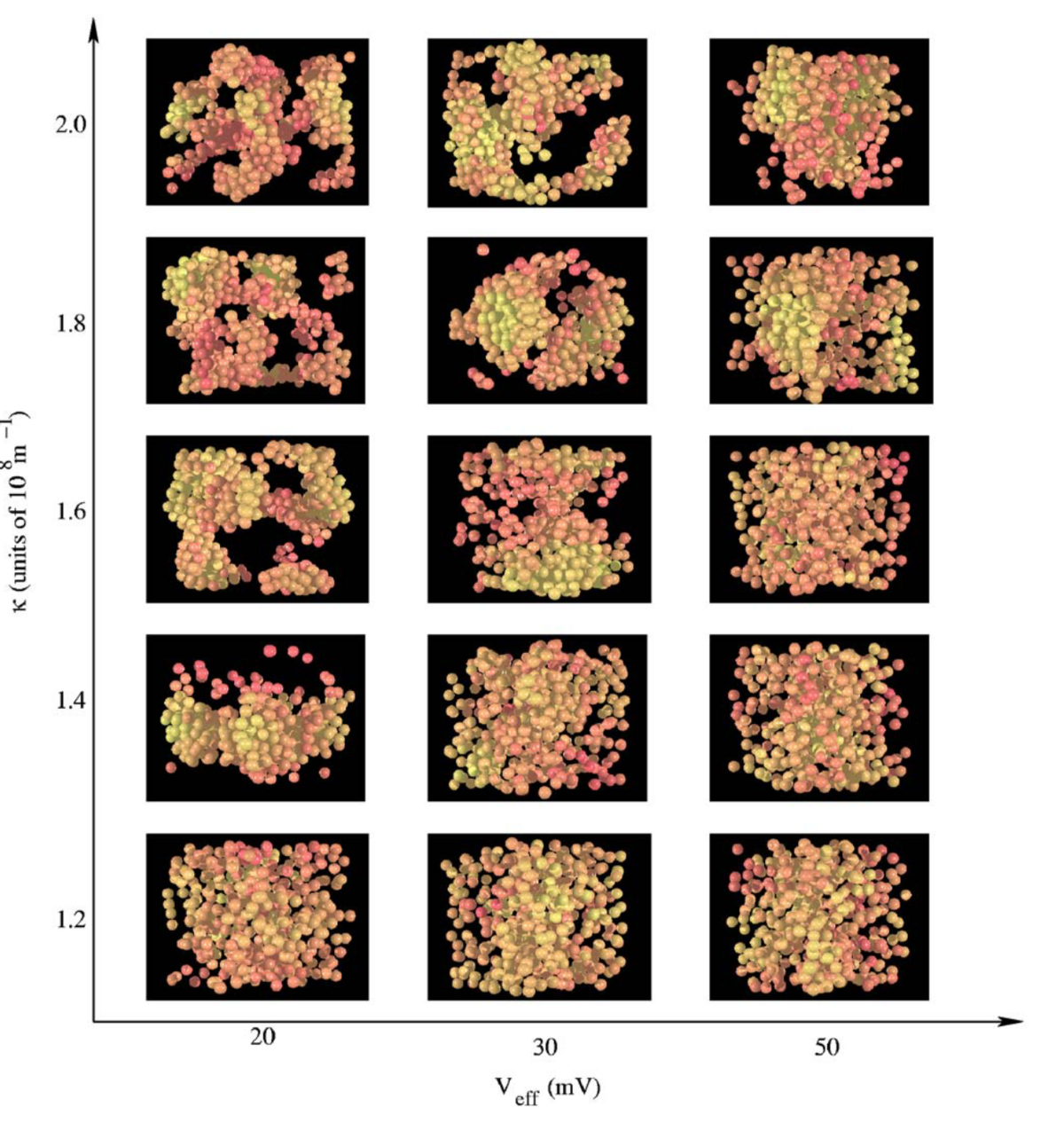
Condensed matter is considered soft, when at least some of the relevant energy scales are comparable with the one set by room temperature or, more generally, when thermal excitations are sufficient to deform or otherwise structurally alter it. Conceptually, this means that entropy is very important and on at least equal relevance as the elastic energies in the system. An instructive example of this is the entropic elasticity of polymeric materials, which is not generated in a simple mechanic way, by extending molecular bonds, but entropically by constraining the thermally fluctuating polymers. One way, an abundance of very soft modes is often generated is by means of disorder. Generally speaking, disorder generates frustration and frustration leads to a high number of states with similar energetic properties.
Computer simulation of complex liquids

Understanding the relation between exact microscopic models and effective mesoscopic dynamics, allows for a peculiar approach to numerical simulations of liquids in a general sense: One can deliberately choose to not integrate the microscopical equations of motions, but instead construct numerically efficient stochastic dynamics algorithms that are guaranteed to lead to the same dynamics on a mesoscopic level. This approach numerically implements the strategy of disregarding uninteresting fast modes in favor of interesting slow modes. The loss of spatio-temporal resolution enables system sizes and gains in computational efficiency.
This approach to simulation of liquids is called multi-particle collision dynamics (MPCD). We contributed fundamentally to this field by way of the stochastic rotation dynamics (SRD) algorithm.
Pattern formation far from equilibrium
A prominent representation of the interesting dynamics that can emerge on meso- to macroscopic scales is pattern formation. The evolution of a system that would statically allow for spatially uniform states, dynamically shows a richer, scale-dependent behaviour. A striking historical example for the counter-intuitiveness that can be involved is the Turing mechanism in reaction-diffusion systems which has for example been used to describe the patterns in animals. Here, the formation of ordered patterns is driven by diffusion, which would be expected to contribute to greater uniformity in the system.
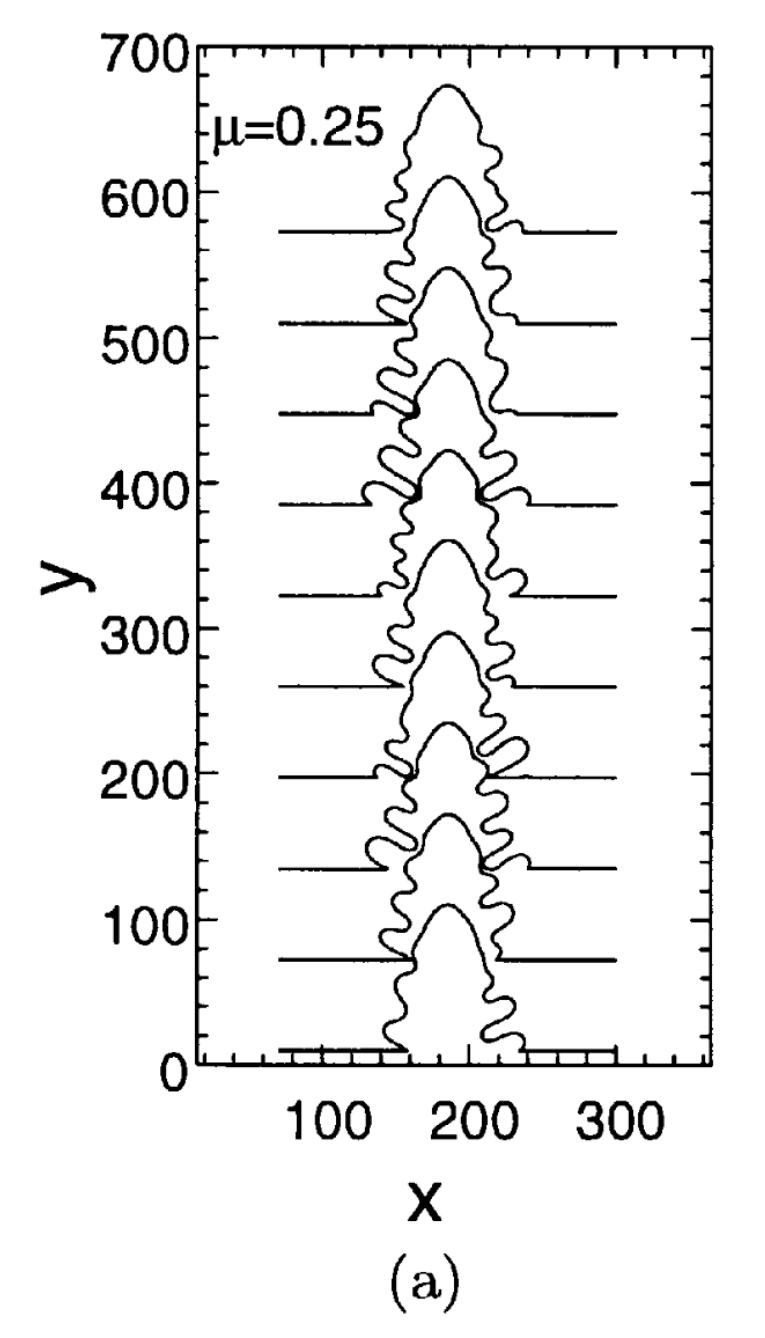
Kinetic roughening, the evolution of structured interfaces due to dynamical instabilities, occurs in a lot of growth or otherwise driven processes. The description of such rough interfaces requires its own (fractal) language, that conceptually resembles the tools used to describe critical systems near a phase-transition. For example, encoding the complex geometry into roughness exponents.
These pattern problems can be fruitful in every of the branches of contemporary physics. We numerically predicted the existence of a novel building block, double-finger structure now called doublon, in phase transitions with diffusion transport by means of front-tracking algorithm. Analytically, describing the selection rules poses an interesting challenge as the highest derivative (the curvature) enters with an asymptotically small prefactor (the surface tension), thus requiring a singular pertubation theory that is conceptually similar to the WKB approach to quantum mechanics. Finally, we were in collaboration with experimentalists from the University of Paris also able to validate the predictions experimentally.
