Wie Wissenschaftler der AG Komplexe Quantensysteme in einer kürzlich in den Physical Review Letters veröffentlichen Arbeit darstellen, wird die gezielte Manipulation von topologischen Randzuständen durch die nicht-Hermitesche Erweiterung der Quantenmechanik ermöglicht. „Nicht-Hermitesche Quantenmechanik“ ist dabei keine theoretische Spielerei: Experimentell sind mechanische, elektrische, akustische oder optische Systeme, die effektiv durch eine Schrödinger-Gleichung mit nicht-Hermiteschem Hamilton-Operator beschrieben werden, von großer Relevanz.
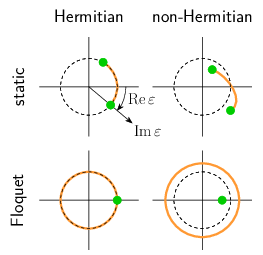
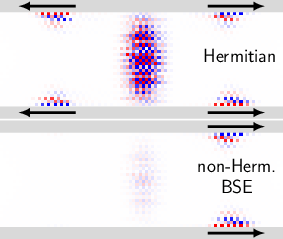
Ein Beispiel sind Gitterstrukturen aus photonischen Wellenleitern, in denen sich die in der Arbeit eingeführte Methode des „boundary state engineering“ unmittelbar realisieren lässt. Die Nicht-Hermitezität trägt dabei den intrinsischen Verlusten in solchen Systemen Rechnung. Die grundlegende Einsicht der aktuellen Arbeit besteht darin, dass die Möglichkeit zur gezielten Manipulation topologischer Randzustände erst aus dem engen Zusammenspiel von nicht-Hermitezität und der Floquet-Dynamik periodisch getriebener Systeme entsteht. Der Grund hierfür besteht darin, dass sich in nicht-Hermiteschen Floquet-Systemen das Spektrum von Randzuständen vollständig vom Spektrum der Volumenzustände ablösen lässt - ein Effekt, der in Hermiteschen oder statischen Systemen verboten ist. Hierdurch können die Eigenschaften von Randzuständen individuell eingestellt werden, ohne dass der topologische Schutz dieser Zustände aufgegeben wird. Damit wird die erwünschte Robustheit der Randzustände erhalten, die oft unnötig engen Einschränkungen, die aus der strikten Äquivalenz von Transport und Topologie folgen, aber aufgebrochen. Außer den praktischen und experimentellen Möglichkeiten, die die gezielte Manipulation von Randzuständen ermöglicht, ergeben sich aus diesem „boundary state engineering“ neue Ansätze zur Beantwortung fundamentaler Fragen der Physik nicht-Hermitescher topologischer Systeme - beispielsweise zur Formulierung einer „bulk-boundary“-Korrespondenz, die die eingeschränkte Äquivalenz von Transport und Topologie quantitativ erfasst, oder zur topologischen Klassifikation nicht-Hermitescher Randzustände.
Originalveröffentlichung:
B. Höckendorf, A. Alvermann, und H. Fehske
„Non-Hermitian Boundary State Engineering in Anomalous Floquet Topological Insulators“
Phys. Rev. Lett. 123, 190403 (2019)
https://link.aps.org/doi/10.1103/PhysRevLett.123.190403
Ansprechpartner:
Bastian Höckendorf
PD Dr. Andreas Alvermann
Prof. Dr. Holger Fehske
Institut für Physik der Universität Greifswald
Felix-Hausdorff-Str. 6
17487 Greifswald
Telefon +49 3834 420 4763
alvermannphysik.uni-greifswaldde
fehskephysik.uni-greifswaldde
https://physik.uni-greifswald.de/arbeitsgruppen/ag-fehske/